Non exact differential equation integrating factor pdf

Non exact differential equation integrating factor pdf
Boyce/DiPrima 9 th ed, Ch 2.6: Exact Equations & Integrating Factors Elementary Differential Equations and Boundary Value Problems, 9 th edition, by William E. Boyce and Richard C. DiPrima, ©2009 by John Wiley & Sons, Inc.
As in the case of classical differential equations, one may reduce the non exact fractional differential equation to be exact using what is called integrating factors. We will consider two cases for the existence of integrating factors.
Integrating Factors . The solution of a homogeneous first-order linear differential equation of the form . where a(x) and b(x) are known functions of x, is easy to find by direction integration.
Ch 2.1: Linear Equations; Method of Integrating Factors A linear first order ODE has the general form where f is linear in y. Examples include equations with
Integrating factor: is exact 5. Linear: 6. Bernoulli equation: y9 1 Psxdy 5 Qsxdyn y9 1 Psxdy 5 Qsxd usx, ydMsx, yddx 1 usx, ydNsx, yddy 5 0 Msx, yddx 1 Nsx, yddy 5 0, ›My›y 5 ›Ny›x Msx, yddx 1 Nsx, yddy 5 0, Msxddx 1 Nsyddy 5 0 Method Form of Equation. 1104 CHAPTER 15 Differential Equations Applications One type of problem that can be described in terms of a differential equation
Such a function μ is called an integrating factor of the original equation and is guaranteed to exist if the given differential equation actually has a solution. Integrating factors turn nonexact equations into exact …
Then α has a non-zero integrating factor This theorem follows from the theory of solutions of ordinary differential equations. Finding the integrating factor may not be an easy matter. However, there is a strategy that may be helpful. 1.3. ORDINARY DIFFERENTIAL EQUATIONS IN TWO DIMENSIONS 5 Recall that if a differential form is exact, then it is closed. So if µ is an integrating factor
13/02/2014 · Section 2.4 End of Lecture – Solving non-Exact ODEs using Integrating Factors.
PDF This note investigates the integrating factors μ of an exact differential equation M dx + N dy = 0 and finds conditions on the potential F under which μ is a function of F.
A clever method for solving differential equations (DEs) is in the form of a linear first-order equation. This method involves multiplying the entire equation by an integrating factor. A linear first-order equation takes the following form: Calculate the integrating factor. Multiply the DE by this
is called an exact differential equation if there exists a function of two variables (uleft( {x,y} right)) with continuous partial derivatives such that

Lesson 29 Exact Differential Equations Integrating Factors

Solving a non exact differential equation given the form
EXACT DIFFERENTIAL EQUATIONS 3 which would be equivalent whenever (x;y) 6= 0. It may be possible to multiply (1) by such a function (x;y) so that the new equation (4) is exact. In that case we would say that (x;y) is an integrating factor for (1). Integrating factors are not so easy to come by. However, they exist in a few cases that are good to know. We will only cover three cases. The rst
an exact one. The function u(x,y) (if it exists) is called the integrating factor. Note that u(x,y) satisfies the following equation: This is not an ordinary differential equation since it involves more than one variable. This is what’s called a partial differential equation. These types of
S. Ghorai 4 4.1 How to nd intgrating factor Theorem 2. If (2) is such that 1 N @M @y @N @x! is a function of xalone, say F(x), then = e R F dx is a function of xonly and is an integrating factor for (2).
Lesson 6: Exact equations Determine whether or not each of equations below are exact. If it is exact find the solution by two methods. 1. (2x+4y)+(2x¡2y)y0 = 0
DIFFERENTIAL EQUATIONS COURSE NOTES, LECTURE 4: EXACT EQUATIONS AND INTEGRATING FACTORS. ANDREW SALCH 1. Exact equations. Suppose you have an equation …
The equation is now homogeneous in X & Y. .*Homogeneous Differential Equation A Differential Equation of the form dy f ( x. *Non –Homogeneous Solve differential Equations (i) To solve dy ax by c dx a’ x b’ y c’ when a b a ‘ b’ Let x=X+h . substitute back the value of u. y ) dx g ( x. ii) To solve dy ax by c dx a’ x b’ y c’ when a b a ‘ b’ Let ax+by=u dy 1 du ( a) dx b dx put the values of ax
PDF In this work we present a simple algorithm for computing integrating factors of certain classes of first order Ordinary Differential Equations (ODE), as well as the foundation of the
3. The method of exact solution of nonlinear differential equations by integrating factors has been examined by considering the solution of the Van der Pohl equation.
2.2 For example, the separable equation ydx+2xdy= 0 is not exact, but after multiplication by 1=(xy) it becomes x −1 dx+2y −1 dy= 0, which is exact. 2.3 Finding an integrating factor …
An integrating factor is something I would try only when an equation doesn’t t any of the other patterns, because the integrating factor technique involves more work than the others.

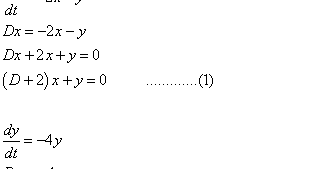
This section provides materials for a session on solving first order linear equations by integrating factors. Materials include course notes, lecture video clips, practice problems with solutions, a problem solving video, and quizzes consisting of problem sets with solutions.
January 19, 2014 5-1 5. Exact Equations, Integrating Factors, and Homogeneous Equations Exact Equations A region Din the plane is a connected open set.
Calculus, Separation of Variables Differential Equations.This resource is designed for Calculus AB, BC and College Calculus 1 or 2, depending upon curriculum. Students solve Separ
1.4 Exact differential equations and Integrating factors 1.5 Linear differential equations and Bernoulli equations 1.6 Orthogonal trajectories of curves 1.7 Existence and uniqueness of solutions 1. First-order Ordinary Differential Equations Advanced Engineering Mathematics 1. First-order ODEs 2 1.1 Basic concepts and ideas Equations 3y2 + y-4 = 0 y = ? where y is an unknown. Functions f(x
Exact Differential Equations: Integrating Factors In general, equations of the type M(x,y)dx+N(x,y) dy = 0are not exact. However, it is sometimes possible to transform the equation into an exact differential equation multi-plying it by a suitable function I(x,y). That is, if I(x,y)is an integrating factor then the differential equation I(x,y)M(x,y)dx+I(x,y)N(x,y)dy=0 becomes exact. A solution
It is commonly used to solve ordinary differential equations, but is also used within multivariable calculus when multiplying through by an integrating factor allows an inexact differential to be made into an exact differential (which can then be integrated to give a scalar field).
Free exact differential equations calculator – solve exact differential equations step-by-step
Integrating Factors.pdf – Download as PDF File (.pdf), Text File (.txt) or view presentation slides online. Scribd is the world’s largest social reading and publishing site. Search Search
non exact differential equation A D.E of the form is said to be Non-Exact D.E if In order to make above D.E to be Exact we have to multiply with which is known as

Differential Equations can be converted into exact equations by multiplying through by a function known as the integrating factor for the equation. In the last part of this Section you will learn how to decide whether an equation is capable of being transformed into an exact equation, how to determine the integrating factor, and how to obtain the solution of the original equation
Exact Differential Equations • Integrating Factors Exact Differential Equations In Section 5.6, you studied applications of differential equations to growth and decay problems. In Section 5.7, you learned more about the basic ideas of differential equa- tions and studied the solution technique known as separation of variables. In this chapter, you will learn more about solving differential
Math 2280 – Lecture 6: Substitution Methods for First-Order ODEs and Exact Equations Dylan Zwick Fall 2013 In today’s lecture we’re going to examine another technique that can be useful for solving first-order ODEs. Namely, substitutuion. Now, as with u-substitutuion from calculus, figuring out the right substitution to make, assuming there even is a right one, is not always obvious. It
Another reason is that exact differential equations are not limited to two variables. You You cansolve P ( x,y,z ) dx + Q ( x,y,z ) dy + R ( x,y,z ) dz =0withthesameapproach,butyoucannot
If you mean an integral factor that converts a non-exact equation into an exact equation, then 2 possibilities are NOT possible. At most you can only have ONE integral factor and in most cases there is no integrating factor.
Total fractional differentials with applications to exact
The differential equation + − − = 0 is a) Not exact b) exact with = − c) exact with = d) homogeneous The differential equation − + − = 0 is a) Not exact b) exact with = − c) exact with = −1 + 2 d) exact There exists a function = , such that = + where and are functions of and . Then which of the following option is always correct for the differential equation + = 0 ? a) = b
This second method that we used is called the integrating factor method. In this case the integrating factor was In this case the integrating factor was the e 3x 2 that we multiplied the equation by.
2.3. EXACT DIFFERENTIAL EQUATIONS 21 2.3 Exact Differential Equations A differential equation is called exact when it is written in the specific form
12/08/2015 · In this video I will review and solve the 1st order differential equation 3x^2-2y^2+(1-4xy)y’= 0 (not requiring an integrating factor). Next video in the Exact Differential series can be seen at
Integrating Factor We multiply both sides of the differential equation by the integrating factor I which is defined as I = e R P dx. General Solution Multiplying our original differential equation by I we get that dy dx +Py = Q ⇔ I dy dx +IPy = IQ ⇔ Z (I dy dx +IPy)dx = Z IQdx ⇔ Iy = Z IQdx since d dx (Iy) = I dy dx +IPy by the product rule. As both I and Q are functions involving
It is sometimes possible to convert a di erential equation that is not exact into an exact equation by multiplying the equation by a suitable integrating factor.
Using an integrating factor to make a differential equation exact If you’re seeing this message, it means we’re having trouble loading external resources on our website. If you’re behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
Once a differential equation M dx + N dy = 0 is determined to be exact, the only task remaining is to find the function f ( x, y) such that f x = M and f y = N. The method is simple: Integrate M with respect to x , integrate N with respect to y , and then “merge” the two resulting expressions to …
Multiply both sides of the given equation by the integrating factor u, the new equation which is uM dx + uN dy = 0 should be exact. Solve the result of Step 6 by exact equation or by inspection . Tags: – birds of vancouver island field guide If has an integrating factor, then it has many (in fact infinitely many) integrating factors. Given ( 7.3.1 ), whether or not it has an integrating factor, is a tough question to settle. In some cases, we use the following rules to find the integrating factors.
Help with solving differential Equation using Exact Equation method 1 finding an integrating factor for the nonlinear non-autonomous ODE $ (xy)y’+yln y – 2xy = 0 $
Help with solving linear differential equations using an integrating factor 1 Finding integrating factor for non-exact differential equation $(4y-10x)dx+(4x-6x^2y^{-1})dy=0$.
Reduction to Exact Form If the differential equation is not exact, Make it to be exact by multiplying ‘ Y Z integrating factors: 1 Y Z EY 2 Y Z EZ ⇒ ‘ Y
In this case, one can try to find an integrating factor which makes the given differential equation exact. [Differential Equations] [Algebra] [Trigonometry ] [Calculus] …
Non – exact differential equations need to be converted into exact differential equations before their solutions can be found, and this can be achieved when we multiple that equation (non – exact differential equation) with the integration factor. The integration factor converts non – exact differential equation to exact differential equation. More often than not, much attention is not
A factor which possesses this property is termed an integrating factor. Since the above analysis is quite general, it is clear that an inexact differential involving two independent variables always admits of an integrating factor.
Problem on Exact Differential Equations. Exact Differential Equation from Non-Exact by using an Integrating Factor. Problem. Given the differential equation-2 xy dx + dy = 0.
In this section we solve linear first order differential equations, i.e. differential equations in the form y’ + p(t) y = g(t). We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor …
Example 3:¶ Show that is not exact. (Solution: in class) As in Example 2, there are cases that given DEs are not exact. In this case, we can possibly convert such non-exact DEs to exact DEs by multiplying a suitable integrating factor.
factor that transforms a non-exact differential equation to an exact one is called an integrating factor . We shall only discuss the procedure for solving a linear non-autonomous first order
8.a Integrating Factors in Di erential Equations 0.0.1
The first equation is usually not exact but multiplying it by the appropriate integrating factor will make it exact, but use of an integrating factor may eliminate solutions or may lead to extraneous solutions.
the equation is not exact. However, we can try to find so-called integrating factor, which is a function (mu left( {x,y} right)) such that the equation becomes exact after multiplication by this factor.
An inexact differential or imperfect differential is a specific type of differential used in thermodynamics to express the path dependence of a particular differential. It is contrasted with the concept of the exact differential in calculus , which can be expressed as the gradient of another function and is therefore path independent.
The method of integrating factors is a technique for solving linear, first order partial differential equations that are not exact. In this lesson, a definition is given for this type of equation
Exact Differential Equations Calculator Symbolab

EXACT EQUATIONS AND INTEGRATING FACTORS Yola
Exact equations and integrating factors. Exact equations intuition 1 (proofy) Exact equations intuition 2 (proofy) Exact equations example 1. Exact equations example 2. This is the currently selected item. Exact equations example 3. Integrating factors 1. Integrating factors 2. Next tutorial. Homogeneous equations. Video transcript. Let’s do some more examples with exact differential equations
2.1 Integrating factors. If the di erential equation

Math 2280 Lecture 6 Substitution Methods for First

Exact equations example 2 (video) Khan Academy

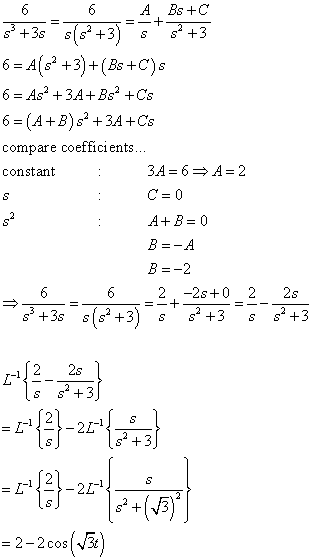
EXACT DIFFERENTIAL EQUATIONS People

https://en.wikipedia.org/wiki/Exact_differential
The Integrating Factors of an Exact Differential Equation
– The Determination of Integrating Factor Elementary
Solution by Integrating Factors Unit I First Order

Solving non-Exact Differential Equations using Integrating

Exact Differential Equations Felderbooks

Solution by Integrating Factors Unit I First Order
Nonexact Equations Integrating Factors Video & Lesson

Differential Equations can be converted into exact equations by multiplying through by a function known as the integrating factor for the equation. In the last part of this Section you will learn how to decide whether an equation is capable of being transformed into an exact equation, how to determine the integrating factor, and how to obtain the solution of the original equation
Using an integrating factor to make a differential equation exact If you’re seeing this message, it means we’re having trouble loading external resources on our website. If you’re behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
3. The method of exact solution of nonlinear differential equations by integrating factors has been examined by considering the solution of the Van der Pohl equation.
2.3. EXACT DIFFERENTIAL EQUATIONS 21 2.3 Exact Differential Equations A differential equation is called exact when it is written in the specific form
13/02/2014 · Section 2.4 End of Lecture – Solving non-Exact ODEs using Integrating Factors.

Exact equations example 2 (video) Khan Academy
Exact Differential Equations Calculator Symbolab

A clever method for solving differential equations (DEs) is in the form of a linear first-order equation. This method involves multiplying the entire equation by an integrating factor. A linear first-order equation takes the following form: Calculate the integrating factor. Multiply the DE by this
factor that transforms a non-exact differential equation to an exact one is called an integrating factor . We shall only discuss the procedure for solving a linear non-autonomous first order
As in the case of classical differential equations, one may reduce the non exact fractional differential equation to be exact using what is called integrating factors. We will consider two cases for the existence of integrating factors.
Ch 2.1: Linear Equations; Method of Integrating Factors A linear first order ODE has the general form where f is linear in y. Examples include equations with
A factor which possesses this property is termed an integrating factor. Since the above analysis is quite general, it is clear that an inexact differential involving two independent variables always admits of an integrating factor.

Differential Equations Integrating Factor – S.O.S. Math
Differential Equations Linear Equations from The Math Pages

the equation is not exact. However, we can try to find so-called integrating factor, which is a function (mu left( {x,y} right)) such that the equation becomes exact after multiplication by this factor.
If has an integrating factor, then it has many (in fact infinitely many) integrating factors. Given ( 7.3.1 ), whether or not it has an integrating factor, is a tough question to settle. In some cases, we use the following rules to find the integrating factors.
Integrating Factors . The solution of a homogeneous first-order linear differential equation of the form . where a(x) and b(x) are known functions of x, is easy to find by direction integration.
1.4 Exact differential equations and Integrating factors 1.5 Linear differential equations and Bernoulli equations 1.6 Orthogonal trajectories of curves 1.7 Existence and uniqueness of solutions 1. First-order Ordinary Differential Equations Advanced Engineering Mathematics 1. First-order ODEs 2 1.1 Basic concepts and ideas Equations 3y2 y-4 = 0 y = ? where y is an unknown. Functions f(x
Using an integrating factor to make a differential equation exact If you’re seeing this message, it means we’re having trouble loading external resources on our website. If you’re behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
Exact Differential Equations • Integrating Factors Exact Differential Equations In Section 5.6, you studied applications of differential equations to growth and decay problems. In Section 5.7, you learned more about the basic ideas of differential equa- tions and studied the solution technique known as separation of variables. In this chapter, you will learn more about solving differential
EXACT DIFFERENTIAL EQUATIONS 3 which would be equivalent whenever (x;y) 6= 0. It may be possible to multiply (1) by such a function (x;y) so that the new equation (4) is exact. In that case we would say that (x;y) is an integrating factor for (1). Integrating factors are not so easy to come by. However, they exist in a few cases that are good to know. We will only cover three cases. The rst
January 19, 2014 5-1 5. Exact Equations, Integrating Factors, and Homogeneous Equations Exact Equations A region Din the plane is a connected open set.
This second method that we used is called the integrating factor method. In this case the integrating factor was In this case the integrating factor was the e 3x 2 that we multiplied the equation by.
2.3. EXACT DIFFERENTIAL EQUATIONS 21 2.3 Exact Differential Equations A differential equation is called exact when it is written in the specific form
The first equation is usually not exact but multiplying it by the appropriate integrating factor will make it exact, but use of an integrating factor may eliminate solutions or may lead to extraneous solutions.